Permutation Pairity
A quick proof that if two sequences of swaps lead to the same overall permutation, the number of swaps must both be even or both be odd (i.e., the number of swaps has the same parity).
First note that any permutation can be broken up into cycles, where a cycle is just N positions all swapping places with each other in a circle.
To see this for any given permutation, just start at the first position, note where it goes, then note where that position goes, and keep going, until you get back to 1. If there are any positions you haven’t touched yet, start the process again starting there.
For example:
-
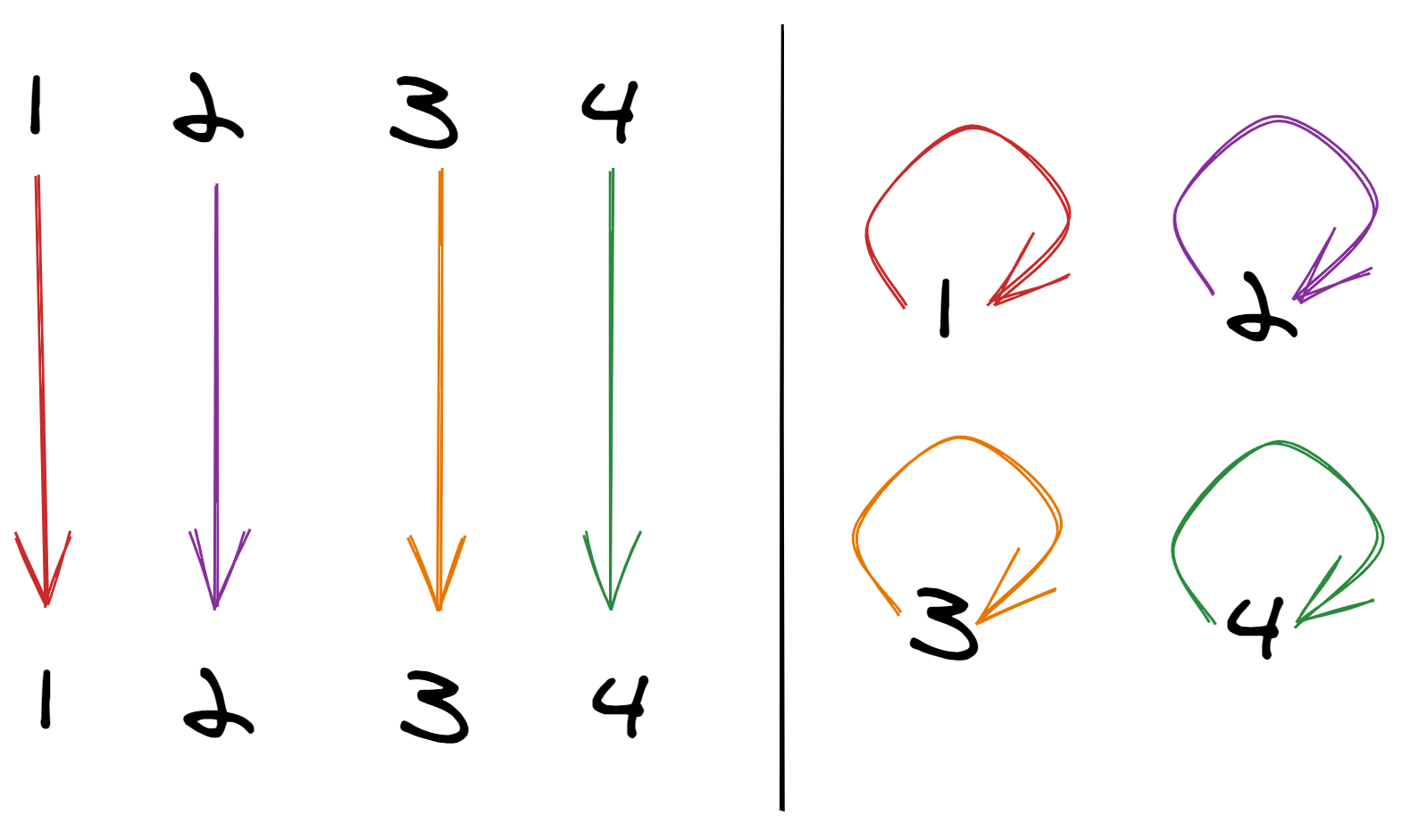
The permutation of 4 elements where everything stays the same is made up of four cycles: 1 swapping with itself, 2 swapping with itself, 3 swapping with itself, and 4 swapping with itself
-
Here, 1 maps to 2, 2 maps to 3, 3 maps to 4, and 4 maps to 1. So this is the single cycle 1 → 2 → 3 → 4
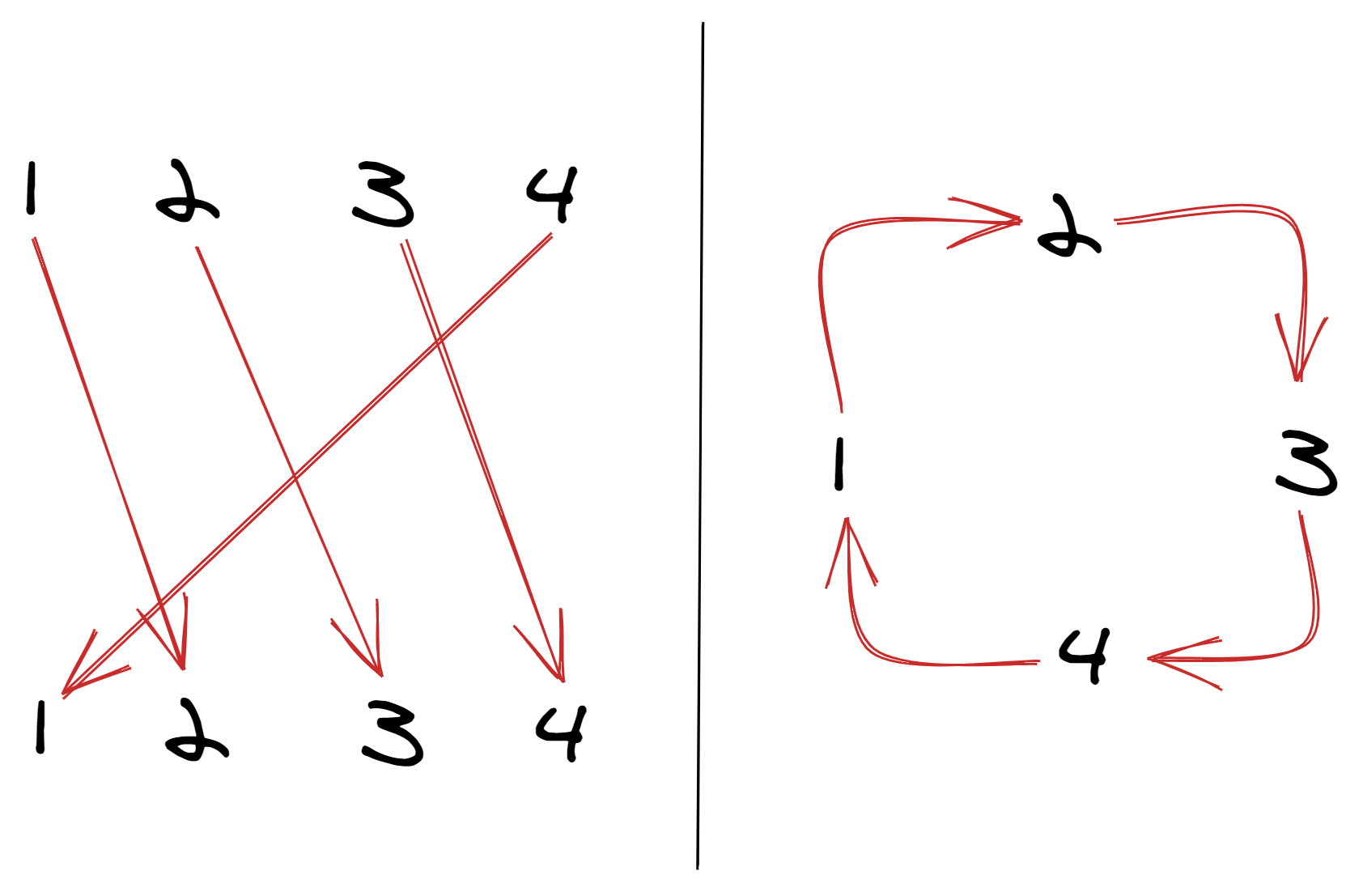
-
In this permutation:
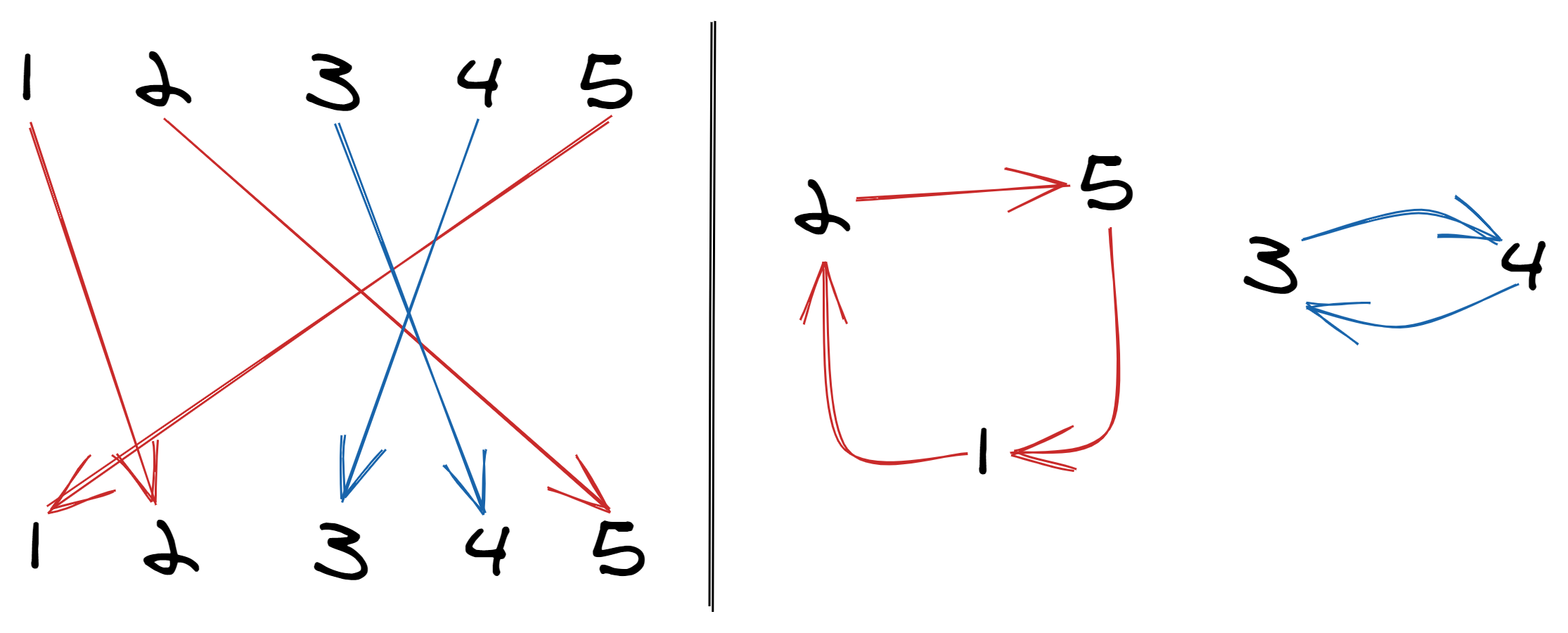
- 1 maps to 2, 2 maps to 5, 5 maps 1; this is the cycle (1 → 2 → 5)
- 4 maps to 3 and 3 maps to 4, which is the cycle (3 → 4)
Importantly, there is just one, unique way to break up any given permutation into cycles.
Now, note that if we take a permutation and swap any two elements, a and b, one of two things happens:
- either a and b were already part of the same cycle, in which case their cycle will split into two
- or, a and b were part of two different cycles, in which case their cycles will join together
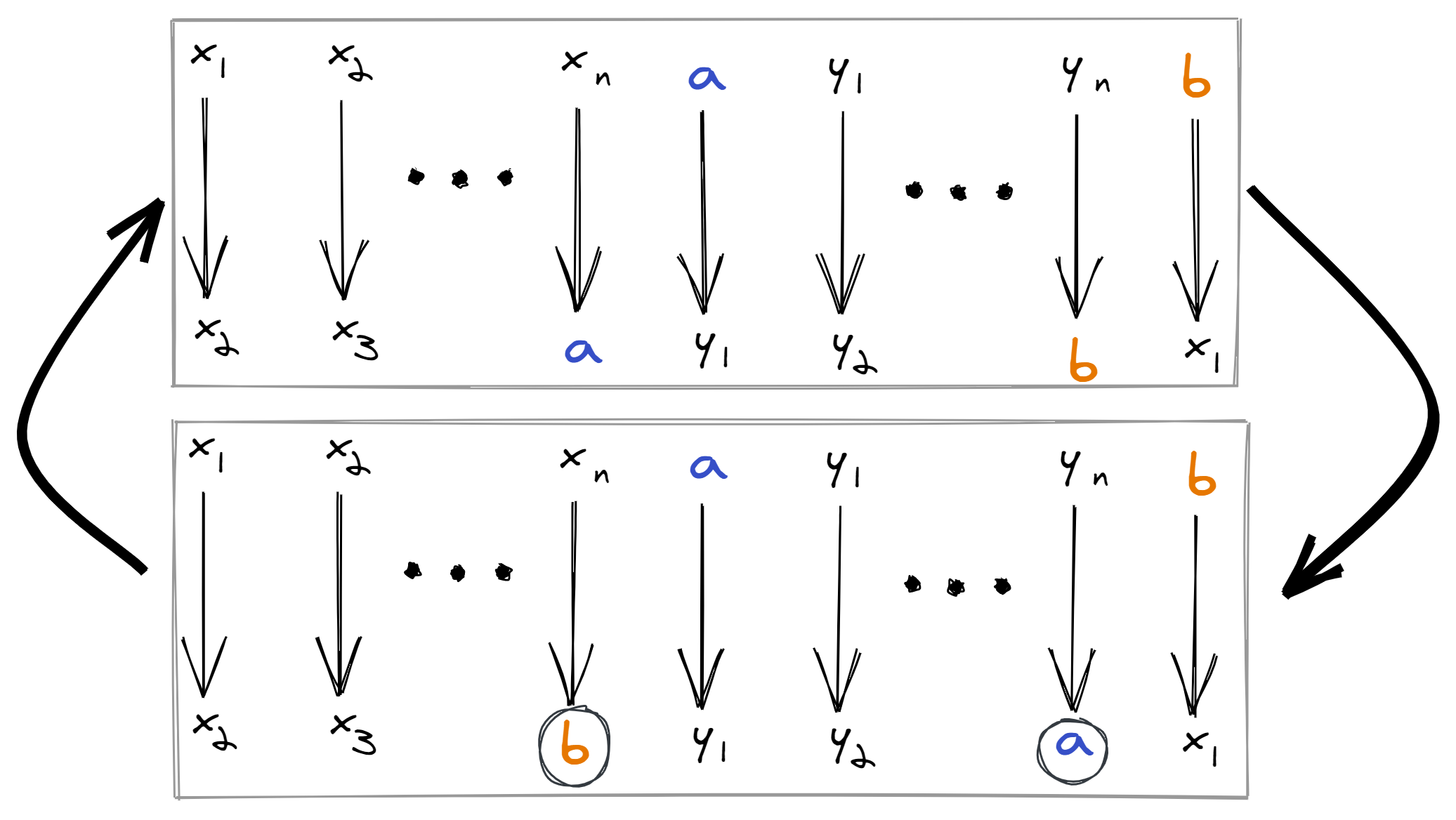
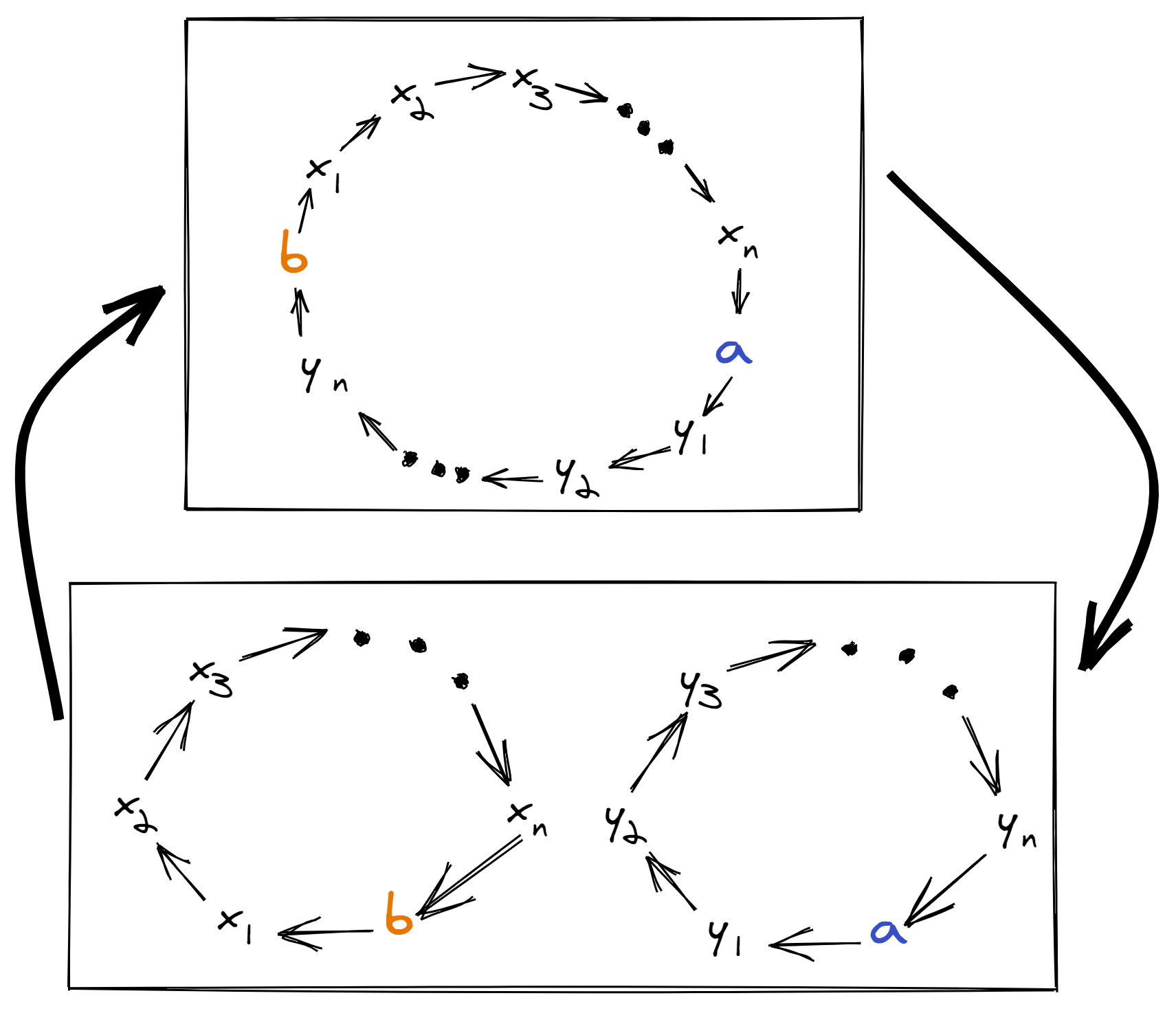
Importantly, the number of cycles always changes (up or down) by exactly one.
And that’s all we need! If we can build up a permutation with N swaps, adding an (N+1)st swap will change the number of cycles by 1, resulting in a different permutation. We need at least an (N+2)nd swap to get us back to the original permutation.
An (N+2)nd swap will either get us back to the correct cycle count, or, put us 2 away from the correct cycle count, which means we need at least an (N+3)rd and an (N+4)th swap to get back to the correct count.
No matter what happens, you always need to add an even number of swaps to get back to the right count, which means the total number of swaps will remain at whatever pairity it was to begin with.
Inspired by Numberphile. Drawings by Excalidraw.
↩ April 26, 2020